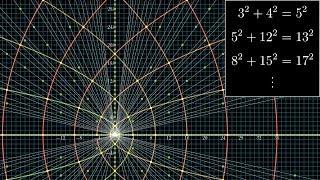
All possible pythagorean triples, visualized

176-57-185 is connected to pair (3,8). 176-57=119=7*17. There are three other subgroups:
(13, 5) ---> 299 180 349
(11, 1) ---> 143 24 145
( 9,10) ---> 261 380 461


| 2 1 2 | | 9 | | 140 |
| 1 2 2 | * | 40 | = | 171 |
| 2 2 3 | | 41 | | 221 |


| - 8 - 9 12 | | 9 | | 60 |
| - 9 - 8 12 | * | 40 | = | 91 |
| -12 -12 17 | | 41 | | 109 |

There's a direct connection between Pythagorean triples and complex numbers:
√(a+b√c) = √((a+√(a²-b²c))/2)+√((a-√(a²-b²c))/2)
c=-1 ---> √(a+bi) = √((a+√(a²+b²))/2)+√((a-√(a²+b²))/2)
For example:
√ (9+40i) = √(( 9+41)/2)+√(( 9-41)/2) = 5+4i
√ (9 -40i) = √(( 9+41)/2) -√(( 9-41)/2) = 5 -4i
√(-9+40i) = √((-9+41)/2)+√((-9-41)/2) = 4+5i
√(-9 -40i) = √((-9+41)/2) -√((-9-41)/2) = 4 -5i

By taking the opposite of a, the coordinates are swapped;
by taking the opposite of b, (a,bi) is mirrored in the x-axis.

I am watching this 3rd time but still learned something new. This time I realised how complex numbers can be interpreted as matrices.

Watching this drunk hits different man

That negative space concept... The inverse, or the anti-, or what you can derive, or posit strictly based on what you can't see, because of what you can see... And then ending in a conundrum the likes of which only math could bestow upon us, what you couldn't see, you now can see.

Like, imagine a black and white photo of a defoliated wooded area taken taken late in the day, and year, with long shadows. Now imagine you could only see black, and not white, or white and not black.... In any case, you'd still be able to see everything, if only one.

Does this mean there are infinite Pythagorean Triples, even if you exclude those same-shape-different-size duplicates?

Could someone please tell me how he graphed the triplets?

And now being warmed up, we do the same for a3+b^3+c^3 = d^3

Thank you again for making this video, I had always wondered why A squared plus B squared was equal to C squared, and The visual that you shared within the first minute was quite impactful.

i dont know if it work for every pithagorean whole triples but if you have a<b<c and b+c = a²/(c-b) then a²+b²=c²

Can it work in a xyz plane graph? While we are at it what would even be the equivalent of a 3 dimensional pythagorean triangle? A special pyramid?

Sufficiently advanced math is no different from magic.

1. If a imaginary number complex is modulus, then modulus 5+12i is 13.
2. The angle in the to possible the real and imaginary numbers, then angle 5+12i is approximately equal 67.38 degrees.

1. If a imaginary number complex is modulus, then modulus is 21+20i is 29.
2. The angle in the to possible the real and imaginary numbers, then angle 21+20i is approximately equal 43.6 degrees.

But why do you need to go to the complex numbers? Isn't the normal version of the graph able to demonstrate it also?

Challange: Do 3x+1

And what about 1^2+i^2=0?

Can anyone comment why are there captions in so many languages but not ENGLISH?

A^2+B^2=C^2,
Finding $principle$ All of ABC Natural numbers ofABC?

Natural numbers are 1 2 3 4 5 6 7 8 9 10 11 12 13...

As the mathematician who finally discovered the formula to generate every possible Pythagorean triple back in 1998 (the Wade-Wade Theorem), I have an immense appreciation for this video. Nice work!

You know technically Fermat’s last theorem is technically far from being true? In fact there are an infinite number of Pythagorean triplets that have exponents above 2.
Just replace either a or b with 0.

Wait nvm im not patient enough

Oh this is very convinient.

Is it possible to write this as an expression?

I always thought that a "Pythagorean triple" was something like 3²+4²+12²=13² (which is true, btw.. )

So all Pythagorean triples are right triangles?

There is linear algebra. And then there is math that turns things into linear algebra.

Great video.

*your

I was disappointed to find that choosing real and imaginary parts both odd results in a multiple of another triple (but with a and b in different order).

finding all the lattice points on an expanded line .. is a task no different to the problem of finding pythagorean triples.

Proof of newton leibtinz formula!!!!

Wrong! No all of them; some of them.

Where is a possible to find a table with all ternes are visualizzate with the risulting explicate too ?

nice

❤❤❤looks like someone is looking for an event horizons there....and an changing point...perhaps a wormhole...a portal...a door...and guess what..that is what..not that easy...yet hey hey...❤❤❤❤❤😂😂🎉🎉😢😮😢😮🎉🎉😂😂😂😅😅😅😅

Any squeared odd is part of Pythagoroan triples.

The reason that raising the exponents of the Pythagorean theorem doesn't work is because the equation was only meant to work in 2 dimensions, hence the exponent of "²". The only way it'll work with exponents of a higher order (at least, in theory,) is by adding extra parts. IE: a³+b³+c³=d³, or a⁴+b⁴+c⁴+d⁴=e⁴, etc. Again, tho, that's just a theory. Feel free to correct me if its not actually a thing.

Ended up here after making a C++ program that used a brute force method to finding Pythagorean triples. Might as well introduce some of the ideas from this video into the program. Thank you for amazing content.
Edit, using 5 + 12i as input (probably affects others) results in -119 + 120i, which has magnitude 169.

I have a challenge make a method. An apparatus that can be applied to equations in a formulas. That can detect the uses of the number 3 as a numerator trickery or deception apparatus through using numerator the tricks. Basically, it will detect and remove and attempt to accomplish the action of the formula in the absence of effects of the number 3 if detected.

This makes my proof/method of deriving non-trivial Pythagorean triples using the difference of two squares seem kinda pathetic