Daniel Nakano: On tilting modules and p-filtrations

Abstract: In this talk, I will start by presenting historical background on the lifting of G-structures on modules for the corresponding Lie algebra. Early work was initiated in the 1960's with fundamental results by Curtis and Steinberg for simple modules. Later questions involving projective modules was studied by Humphreys-Verma, Ballard and Jantzen.

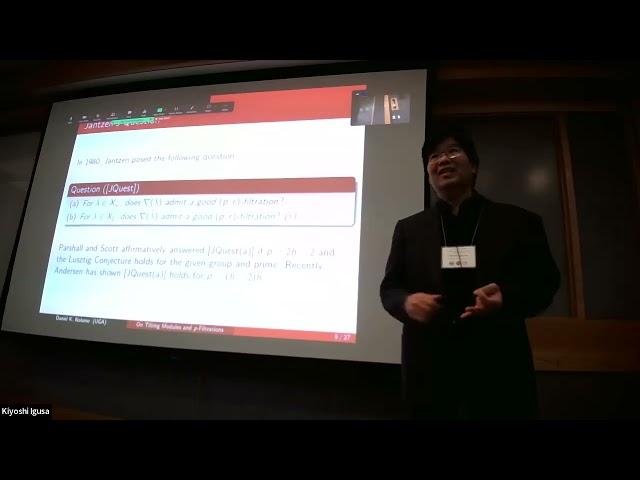
I will then present background material on two conjectures formulated by Donkin at MSRI in 1990. The first conjecture is Donkin's Tilting Module Conjecture (DTilt), and the second conjecture is Donkin’s p-Filtration Conjecture (DFilt). Recent progress by Kildetoft-Nakano and Sobaje has shown that there are important connections between these conjectures. In particular, Jantzen's Question posed in 1980 on the existence of Weyl p-filtrations for Weyl modules for a reductive algebraic group constitutes a central part of the new developments.

I will describe how we produced infinite families of counterexamples to Jantzen’s Question and Donkin’s Tilting Module Conjecture. New techniques to exhibit explicit examples are provided along with methods to produce counterexamples in large rank from counterexamples in small rank. Counterexamples can be produced via our methods for all groups other than when the root system is of type A_n or B_2. Later, I will also present a complete answer to Donkin’s Tilting Module Conjecture for rank 2 groups.

These results represent joint work with Christopher Bendel, Cornelius Pillen and Paul Sobaje.

Recorded at the Maurice Auslander International Conference, Woods Hole Oceanographic Institute, 2023.

Скачать видео