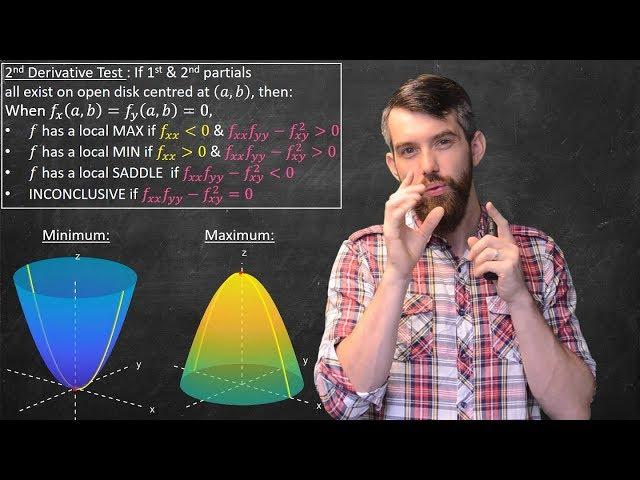
Multi-variable Optimization & the Second Derivative Test

Finding Maximums and Minimums of multi-variable functions works pretty similar to single variable functions. First,find candidates for maximums/minimums by finding critical points. Critical Points are where the partial derivatives with respect to x and y are both zero. Then we classify each critical point using the second derivative test. In the multivariable case, there is a new option beyond max/min/neither, there is also the case of the saddle point. The second derivative test involves computing the Hessian, the determinant of a matrix that helps decide whether points are maximums/minimums/saddle or inconclusive. We sketch the geometric intuition behind the Hessian.

****************************************************
YOUR TURN! Learning math requires more than just watching videos, so make sure you reflect, ask questions, and do lots of practice problems!
****************************************************
►Full Multivariable Calculus Playlist: https://www.youtube.com/playlist?list=PLHXZ9OQGMqxc_CvEy7xBKRQr6I214QJcd

****************************************************
Other Course Playlists:

►CALCULUS I: https://www.youtube.com/playlist?list=PLHXZ9OQGMqxfT9RMcReZ4WcoVILP4k6-m

► CALCULUS II: https://www.youtube.com/playlist?list=PLHXZ9OQGMqxc4ySKTIW19TLrT91Ik9M4n

►DISCRETE MATH: https://www.youtube.com/playlist?list=PLHXZ9OQGMqxersk8fUxiUMSIx0DBqsKZS

►LINEAR ALGEBRA: https://www.youtube.com/playlist?list=PLHXZ9OQGMqxfUl0tcqPNTJsb7R6BqSLo6

***************************************************

► Want to learn math effectively? Check out my "Learning Math" Series:
https://www.youtube.com/watch?v=LPH2lqis3D0&list=PLHXZ9OQGMqxfSkRtlL5KPq6JqMNTh_MBw


►Want some cool math? Check out my "Cool Math" Series:
https://www.youtube.com/playlist?list=PLHXZ9OQGMqxelE_9RzwJ-cqfUtaFBpiho

****************************************************
►Follow me on Twitter: http://twitter.com/treforbazett

*****************************************************

This video was created by Dr. Trefor Bazett. I'm an Assistant Teaching Professor at the University of Victoria.

BECOME A MEMBER:
►Join: https://www.youtube.com/channel/UC9rTsvTxJnx1DNrDA3Rqa6A/join

MATH BOOKS & MERCH I LOVE:
► My Amazon Affiliate Shop: https://www.amazon.com/shop/treforbazett

Тэги:

#Math #Solution #Example #Maximum #Minimum #Optimize #Optimization #Saddle_Point #Critical_Point #Hessian #Second_Derivative_Test #2nd_Derivative_Test #3D #multi-variable #matrix #partials

Скачать видео