Jocelyn Thiebaut: On the approximation hardness of geodetic set and its variants

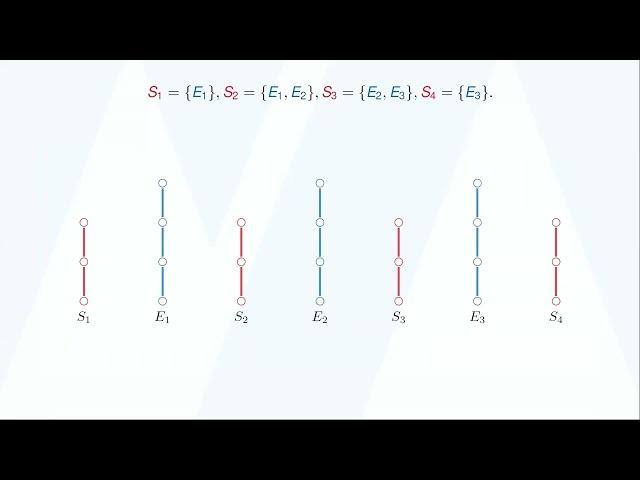
Given a graph G, a geodetic set (resp. edge geodetic set) is a subset X of its vertices such that every vertex (resp. edge) of G is on a shortest path between two vertices of X. A strong geodetic set is a subset X of vertices AND a choice of a shortest path for every pair of vertices of X such that every vertex is on one of these shortest paths. The geodetic number (resp. edge geodetic number) of a graph is the minimum size of a geodetic set (resp. edge geodetic set) and the strong geodetic number is the minimum size of a strong geodetic set. In this work we prove that geodetic number and edge geodetic number are both LOG-APX-hard, even on subcubic bipartite graphs with arbitrarily high girth. Then, we show that there is no 781/780 polynomial-time approximation algorithm for strong (edge) geodetic number, even on subcubic bipartite graphs with arbitrarily high girth. We also prove that, given a subset of vertices, it is NP-hard to determine whether it is a strong geodesic set. Therefore, it is natural to study the problem of maximizing the number of covered vertices by a choice of a shortest path for every pair of a provided subset of vertices. We provide a tight 2-approximation algorithm to solve this problem. Finally, we disprove a conjecture of Iršič and Konvalinka by proving that the strong geodetic number can be computed in polynomial time in complete multipartite graphs.

Joint work with Tom Davot and Lucas Isenmann.

Скачать видео