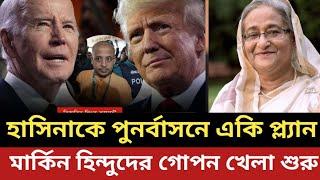
Pyramide Aufgabe – Rechteckige Grundfläche

Nicht so elegant wie sonst – hat mich aber trotzdem interessiert. Allerdings mag ich keine Rätsel, bei denen ein Taschenrechner im Spiel ist!

Gut gemacht, sehr schön. Nur das Ergebnisse 2 mal unterstrichen werden, aber Susanne lernt es nicht mehr und will auch nicht.🧐🤨

Verstanden! Und das reicht mir als Schüler. :)
Scheiß auf die Antworten von Leuten, die meinen es besser, eleganter machen, oder eine Lösung doppelt unterstreichen würden . Mir ist am meisten der Weg zur Lösung wichtig, was absolut gelungen ist. :) Auch die rechnerischen Wege sind absolut verständlich gestaltet. ❤ Liebe Grüße.❤

Wie ist das heute in der Schule. Muss man die Negative Wurzel bei einer Seitenhöhe angeben?

Hallo Susanne
Eine sehr schönes Aufgsbe!
Ich wünsche mir noch eine ähnliche Aufgabe, bei der sich die Pyramidenspitze nicht senkrecht über der Mitte der Grundfläche befindet.

Wieder sehr schön und verständlich erklärt 👍😃

🙏🙂👍

Ich empfehle, stets mit den exakten Werten, also in dem Fall √68 und √73, weiterzurechnen bis zum Schluß, um den Rundungsfehler so klein wie möglich zu halten.

Sehr schöne Aufgabe, und wunderbar gelöst, danke!
Mantelfläche, Oberfläche Pyramide: 4(√73 + 3√17) bzw. 4(√73 + 3√17 + 6)
Seitenhöhen: PN = 2√17; QN = √73
Wer's etwas umständlicher mag:
φ = 30°; ∎ABCD → AB = AP + BP = 3 + 3 = CD = 6; BC = BQ + CQ = 2 + 2 = AD = 4
sin⁡(ABC) = sin⁡(BCD) = sin⁡(3φ) = 1 → AC = 2√13 = AM + CM = √13 + √13; MN = h = 8
sin⁡(AMN) = 1 → AN = BN = CN = DN = √(13 + 64) = √77; BNA = CND = θ; CNB = DNA = δ →
36 = 154(1 - cos⁡(θ)) → cos⁡(θ) = 59/77 → sin⁡(θ) = √(1 - cos^2(θ)) = 12√17/77
16 = 154(1 - cos⁡(δ)) → cos⁡(δ) = 69/77 → sin⁡(δ) = √(1 - cos^2(δ)) = 4√73/77 →
Mantelfläche Pyramide = 77(sin⁡(θ) + sin⁡(δ)) = 4(√73+ 3√17) ≈ 83,653 = k →
Oberfläche Pyramide = k + 24 ≈ 107,653
Wer auf den Taschenrechner verzichten will, kann √153 bzw. √73 näherungsweise bestimmen,
hier mit nur einer Iteration:
153 = 9(17) → √153 = 3√17 → 4^2 < 17 → (4 + x)^2 = 17 → x^2 → 0 →
x = 1/8 → 4 + x = 33/8 ≈ √17 → 3√17 ≈ 99/8
8^2 < 73 < 9^2 → (8 + y)^2 = 73 → y^2 → 0 → y = 9/16 → 8 + y = 137/16 →
3√17 + √73 ≈ (1/4)(198 + 137) = 83,75 → 83,75/k = 1,001159 = vertretbare Näherungsabweichung

👍

Mein Lösungsvorchlag ▶
a= 6 m
b= 4 m
h= 8

a) Für die Seitenhöhe, da es sich um eine Pyramide mit rechteckiger Grundfläche handelt, sind zwei Seitenhöhen vorhanden: eine in Richtung der Länge (a) und eine in Richtung der Breite (b):
h= 8 m
a/2= 3 m
Nach dem Satz von Pythagoras:
(a/2)²+h²= hs₁²
3²+8²= hs₁²
hs₁²= 9+64
hs₁= √73 m
hs₁≈ 8,544 m

Nach der Breite, b
h=8 m
b/2= 2 m
Nach dem Satz von Pythagoras:
(b/2)²+h²= hs₂²
2²+8²= hs₂²
hs₂= √4+64
hs₂ ≈ 8,25 m

b) Manteoloberfläche, M
M= 2*A₁+2*A₂
M= 2*b*hs₁/2 + 2*a*hs₂/2
M= bhs₁+ahs₂
M= 4*8,544 + 6*8,25
M= 83,68 m²

c) die Oberfläche, O
O= A+M
A= a*b
A= 6*4
A= 24 m²

O= 24+83,68
O= 107,68 m²

d) Volumen= V
V= A*h/3
V= 24*8/3
V= 8*8
V= 64 m³

DANKE Susanne:)

107,6532825mxm 😅👍🏻

Nur wie berechnet man den Volumen inhalt?😮 nun?

Und jetzt noch das Volumen.

Hör bitte damit auf, den Schülern, die hier zuschauen, beizubringen, mit gerundeten Zwischenergebnissen weiter zu rechnen. Schon mal was von Fehlerfortpflanzung gehört? Erst kürzlich hast du dir damit in einem Video eine Abweichung von rund 0,5 im Endergebnis eingehandelt, was für eine Rundungsdifferenz viel ist. Eigentlich passt das auch gar nicht zu dir: Bei den Herleitungen bist du immer so ausführlich und detailliert, und beim Ausrechnen wirst du dann so unsauber und schludrig?
Leute, tut euch selbst einen Gefallen und rechnet bei sowas mit den exakten Werten weiter, hier also mit √73 und √68, und rundet erst das Endergebnis wieder. Mit gerundeten Zwischenergebnissen weiter zu rechnen ist eine mathematische Todsünde!
PS: Bei den Berechnungen der Dreiecksflächen mit den gerundeten Seitenhöhen finde ich auch ein bisschen weird, dass du da anfängst, vom Taschenrechner zu erzählen; das sind doch wohl Multiplikationen, die man im Kopf hinbekommen sollte.

Können Studenten in Deutschland einen Taschenrechner benutzen? In meinem Heimatland wir können nicht einen Taschenrechner benutzen. Wir mussen die Lösungen als z.B. √68 schreiben.

Mein Ansatz war wie so oft simpler. Die gegenüberliegenden Dreiecksseiten ergeben zusammen immer ein Rechteck. Hierzu brauchen wir nur die jeweilige Mittelhöhe des Dreiecks mittels Pythagoras. So ist es schnell in max. 1 Minute errechnet. Great fun as always!

Mit ihr in einem Raum, da brauchste deinen Staubsauger für die nächste Zeit auf jeden Fall mal nicht mehr. Aber schöne Aufgabe.

Machte wieder Spaß 👍

Leider hat Susanne zu meinem Vorschlag: Pyramide berechnen, bei der die Spitze nicht oberhalb der Mitte der Grundfläche ist, nicht geantwortet.

Oh wie schön wenn man die Aufgaben easy löst und nicht Depressionen bekommt, weil man alles verlernt hat mit dem Alter 😅😊

Zur Aufgabenstellung: Die Grundfläche hat keine Höhe!😊

Lösung:
sl = Seitenhöhe der Dreiecksfläche mit der langen Grundseite a=6
= √[(halbe kurze Grundseite b=4)²+h²]
= √[2²+8²] = √68 ≈ 8,2462
sk = Seitenhöhe der Dreiecksfläche mit der kurzen Grundseite b=4
= √[(halbe lange Grundseite a=6)²+h²]
= √[3²+8²] = √73 ≈ 8,5440
Mantelfläche = 2*6*√68/2+2*4*√73/2 = 6*√68+4*√73 ≈ 83,6533
Oberfläche = Mantelfläche + Grundrechteck = 83,6533+6*4 = 107,6533